Om målet med standardavvikelsen är att sammanfatta spridningen av en symmetrisk datamängd (dvs. i allmänhet hur långt varje referens är från medelvärdet), behöver vi en bra metod för att definiera hur denna spridning ska mätas.

Fördelarna med kvadrering inkluderar:

• Kvadrat ger alltid ett positivt värde, så summan blir inte noll.
• Kvadrat betonar större skillnader — en funktion som visar sig vara både bra och dåligt (tänk på effekten som avvikare har).

Kvadrering har dock ett problem som ett mått på spridning och det är att enheterna alla är kvadrerade, medan vi kanske föredrar att spridningen är i samma enheter som de ursprungliga uppgifterna (tänk på kvadratpund, kvadratdollar eller fyrkantiga äpplen). Därför tillåter kvadratroten oss att återgå till de ursprungliga enheterna.

Jag antar att du kan säga att absolut skillnad tilldelar lika vikt för spridningen av data medan kvadrering betonar ytterligheterna. Tekniskt men som andra har påpekat gör kvadrering algebra mycket lättare att arbeta med och erbjuder egenskaper som den absoluta metoden inte gör (till exempel är variansen lika med det förväntade värdet av fördelningens kvadrat minus kvadratet av medelvärdet för distributionen

Det är dock viktigt att notera att det inte finns någon anledning du kunde inte ta den absoluta skillnaden om det är din preferens för hur du vill se "spridning" (typ av hur vissa människor ser 5% som något magiskt tröskelvärde för $ p $ -värden, när det faktiskt är situationberoende) . Det finns faktiskt flera konkurrerande metoder för att mäta spridning.

Min åsikt är att använda de kvadratiska värdena eftersom jag gillar att tänka på hur det relaterar till Pythagoras statistiksats: $ c = \ sqrt {a ^ 2 + b ^ 2} $ ... detta hjälper mig också att komma ihåg att när arbetar med oberoende slumpmässiga variabler, avvikelser lägger till, standardavvikelser inte. Men det är bara min personliga subjektiva preferens som jag oftast bara använder som minneshjälp, tveka inte att ignorera denna punkt.

En mycket mer ingående analys kan läsas här.

Den kvadratiska skillnaden har trevligare matematiska egenskaper; det är kontinuerligt differentierbart (trevligt när du vill minimera det), det är en tillräcklig statistik för den Gaussiska distributionen, och det är (en version av) L2-normen som är användbar för att bevisa konvergens och så vidare.

Den genomsnittliga absoluta avvikelsen (den absoluta värdenotationen du föreslår) används också som ett mått på spridning, men den är inte så "väluppfostrad" som det kvadratfelet.

Ett sätt du kan tänka dig är att standardavvikelsen liknar ett "avstånd från medelvärdet".

Jämför detta med avstånd i euklidiskt utrymme - detta ger dig det verkliga avståndet, där det du föreslog (vilket, btw, är absolut avvikelse) är mer som en manhattan avstånd beräkning.

anledningen för att vi beräknar standardavvikelse istället för absolut fel är att vi antar att felet ska vara normalfördelat . Det är en del av modellen.

Antag att du mätte mycket små längder med en linjal, då är standardavvikelse ett dåligt värde för fel eftersom du vet att du aldrig kommer att mäta en negativ längd av misstag. Ett bättre mått skulle vara att hjälpa till att anpassa en gammafördelning till dina mätningar:

$ \ log (E (x)) - E (\ log (x)) $

Gilla standardavvikelsen, detta är också icke-negativt och differentierbart, men det är en bättre felstatistik för detta problem.

Svaret som bäst tillfredsställde mig är att det faller ut naturligt från generaliseringen av ett prov till ett n-dimensionellt euklidiskt utrymme. Det kan verkligen diskuteras om det är något som ska göras, men i alla fall:

Antag att dina $ n $ -mätningar $ X_i $ är var och en en axel i $ \ mathbb R ^ n $. Då definierar dina data $ x_i $ en punkt $ \ bf x $ i det utrymmet. Nu kanske du märker att data är mycket lika varandra, så du kan representera dem med en enda platsparameter $ \ mu $ som är begränsad att ligga på linjen definierad av $ X_i = \ mu $. Att projicera din datapunkt på den här raden ger dig $ \ hat \ mu = \ bar x $, och avståndet från den projicerade punkten $ \ hat \ mu \ bf 1 $ till den faktiska datapunkten är $ \ sqrt {\ frac {n-1 } n} \ hat \ sigma = \ | \ bf x- \ hat \ mu \ bf 1 \ | $.

Detta tillvägagångssätt ger dig också en geometrisk tolkning för korrelation, $ \ hat \ rho = \ cos \ vinkel (\ vec {\ bf \ tilde x}, \ vec {\ bf \ tilde y}) $.

Kvadrering av skillnaden från medelvärdet har ett par anledningar.

• Varians definieras som det andra avvikelsemomentet (RV här är $ (x- \ mu) $) och därmed kvadraten som ögonblick är helt enkelt förväntningarna på högre slumpmässiga krafter hos den slumpmässiga variabeln.

• Att ha en kvadrat i motsats till absolutvärdesfunktionen ger en fin kontinuerlig och differentierbar funktion (absolut värde är inte differentierbart vid 0) - vilket gör det till det naturliga valet, särskilt i samband med uppskattning och regressionsanalys.

• Den kvadrerade formuleringen faller också naturligt ur parametrar för normalfördelningen.

Bara så att folk vet, det finns en Math Overflow-fråga om samma ämne.

Varför-är-det-så-coolt-till-kvadrat-nummer-i termer av -finding-the-standard-deviation

Take away-meddelandet är att användning av kvadratroten av variansen leder till enklare matematik. Ett liknande svar ges av Rich och Reed ovan.

Ytterligare en anledning (utöver de utmärkta ovan) kommer från Fisher själv, som visade att standardavvikelsen är mer "effektiv" än den absoluta avvikelsen. Här har effektiv att göra med hur mycket en statistik kommer att fluktuera i värde på olika provtagningar från en befolkning. Om din population normalt är fördelad, kommer standardavvikelsen för olika prover från den populationen i genomsnitt att ge dig värden som är ganska lika varandra, medan den absoluta avvikelsen ger dig siffror som sprids lite mer. Nu är det uppenbarligen under perfekta förhållanden, men den anledningen övertygade många (tillsammans med matematiken som renare), så de flesta arbetade med standardavvikelser.

$ \ newcommand {\ var} {\ operatorname {var}} $ Varians är additiva: för oberoende slumpmässiga variabler $ X_1, \ ldots, X_n $, $$ \ var (X_1 + \ cdots + X_n) = \ var ( X_1) + \ cdots + \ var (X_n). $$

Lägg märke till vad detta möjliggör: Säg att jag kastar ett rättvist mynt 900 gånger. Vad är sannolikheten för att antalet huvuden jag får är mellan 440 och 455 inklusive? Hitta bara det förväntade antalet huvuden ($ 450 $) och variansen av antalet huvuden ($ 225 = 15 ^ 2 $), hitta sedan sannolikheten med en normal (eller Gaussisk) fördelning med förväntan $ 450 $ och standardavvikelse $ 15 $ är mellan $ 439,5 $ och $ 455,5 $. Abraham de Moivre gjorde detta med myntkast på 1700-talet och visade därmed först att den klockformade kurvan är värt något.

Jag tror att kontrasten mellan att använda absoluta avvikelser och kvadratiska avvikelser blir tydligare när man går bortom en enda variabel och tänker på linjär regression. Det finns en trevlig diskussion på http://en.wikipedia.org/wiki/Least_absolute_deviations, särskilt avsnittet "Contrasting Least Squares with Minst Absolute Deviations", som länkar till några studentövningar med en snygg uppsättning applets på http://www.math.wpi.edu/Course_Materials/SAS/lablets/7.3/73_choices.html.

Sammanfattningsvis är minsta absoluta avvikelser mer robusta för avvikare än vanliga minsta kvadrater, men det kan vara instabilt (liten förändring i till och med ett enda datum kan ge stor förändring i monterad linje) och har inte alltid en unik lösning - det kan finnas en hel rad monterade linjer. Även minst absoluta avvikelser kräver iterativa metoder, medan vanliga minsta kvadrater har en enkel lösning med sluten form, men det är naturligtvis inte så stort nu som det var under Gauss och Legendres tid.

Det finns många anledningar; förmodligen är det viktigaste att det fungerar bra som parameter för normalfördelning.

Uppskattning av standardavvikelsen för en distribution kräver att du väljer ett avstånd.
Något av följande avstånd kan användas:

$$ d_n ((X) _ {i = 1, \ ldots , I}, \ mu) = \ left (\ sum | X- \ mu | ^ n \ right) ^ {1 / n} $$

Vi använder vanligtvis det naturliga euklidiska avståndet ($ n = 2 $), som är den som alla använder i det dagliga livet. Avståndet du föreslår är det med $ n = 1 $.
Båda är bra kandidater men de är olika.

Man kan besluta att också använda $ n = 3 $.

Jag är inte säker på att du kommer att tycka om mitt svar, min poäng i motsats till andra är inte att visa att $ n = 2 $ är bättre. Jag tror att om du vill uppskatta en standardavvikelse för en distribution kan du absolut använda ett annat avstånd.

På många sätt hoppar användningen av standardavvikelse för att sammanfatta spridning till en slutsats. Man kan säga att SD implicit antar en symmetrisk fördelning på grund av dess lika behandling av avståndet under medelvärdet som avståndet över medelvärdet. SD är förvånansvärt svårtolkad för icke-statistiker. Man kan hävda att Ginis genomsnittliga skillnad har en bredare tillämpning och är betydligt mer tolkbar. Det kräver inte att man förklarar sitt val av ett mått på central tendens som användningen av SD gör för medelvärdet. Ginis genomsnittliga skillnad är den genomsnittliga absoluta skillnaden mellan två olika observationer. Förutom att det är robust och lätt att tolka råkar det vara 0,98 lika effektivt som SD om distributionen faktiskt var gaussisk.

Det beror på vad du pratar om när du säger "spridning av data". För mig kan detta betyda två saker:

1. Bredden på en samplingsfördelning
2. Noggrannheten för en given uppskattning

För punkt 1) det finns ingen särskild anledning att använda standardavvikelsen som ett mått på spridning, förutom när du har en normal samplingsfördelning. Måttet $ E (| X- \ mu |) $ är ett lämpligare mått i fallet med en distribution av Laplace Sampling. Min gissning är att standardavvikelsen används här på grund av intuition som överförs från punkt 2). Förmodligen också på grund av framgången med modellering av minsta kvadrater i allmänhet, för vilken standardavvikelsen är lämpligt mått. Förmodligen också för att beräkna $ E (X ^ 2) $ i allmänhet är enklare än att beräkna $ E (| X |) $ för de flesta distributioner.

Nu, för punkt 2) finns det en mycket bra anledning att använda variansen / standardavvikelsen som mått på spridning, i ett särskilt men mycket vanligt fall. Du kan se det i Laplace-approximationen till en bakre del. Med Data $ D $ och tidigare information $ I $, skriv den bakre för en parameter $ \ theta $ som:

$$ p (\ theta \ mid DI) = \ frac {\ exp \ left ( h (\ theta) \ höger)} {\ int \ exp \ vänster (h (t) \ höger) \, dt} \; \; \; \; \; \; h (\ theta) \ equiv \ log [ p (\ theta \ mid I) p (D \ mid \ theta I)] $$

Jag har använt $ t $ som en dummyvariabel för att indikera att nämnaren inte är beroende av $ \ theta $ . Om den bakre har ett enda väl avrundat maximalt (dvs inte för nära en "gräns"), kan vi taylor utöka loggsannolikheten om dess maximala $ \ theta_ \ max $. Om vi ​​tar de två första termerna av taylor-expansionen får vi (använder prime för differentiering):

$$ h (\ theta) \ approx h (\ theta_ \ max) + (\ theta_ \ max- \ theta) h '(\ theta_ \ max) + \ frac {1} {2} (\ theta_ \ max- \ theta) ^ {2} h' '(\ theta_ \ max) $$

Men vi har här att eftersom $ \ theta_ \ max $ är ett "väl avrundat" maximum, $ h '(\ theta_ \ max) = 0 $, så har vi:

$$ h (\ theta) \ approx h (\ theta_ \ max) + \ frac {1} {2} (\ theta_ \ max- \ theta) ^ {2} h '' (\ theta_ \ max) $$

Om vi ​​kopplar in den här approximationen får vi:

$$ p (\ theta \ mid DI) \ approx \ frac {\ exp \ left (h (\ theta_ \ max) + \ frac {1} {2} (\ theta_ \ max- \ theta) ^ {2} h '' (\ theta_ \ max) \ höger)} {\ int \ exp \ left (h (\ theta_ \ max) + \ frac {1} {2} (\ theta_ \ max-t) ^ {2} h '' (\ theta_ \ max) \ höger) \, dt} $$

$$ = \ frac {\ exp \ left (\ frac {1} {2} (\ theta_ \ max- \ theta) ^ {2} h '' (\ theta_ \ max) \ höger)} {\ int \ exp \ left (\ frac {1} {2} (\ theta_ \ max-t) ^ {2} h '' (\ theta_ \ max) \ höger) \, dt} $$

Vilket, men för notation är en normalfördelning, med medelvärdet lika med $ E (\ theta \ mid DI) \ approx \ theta_ \ max $ och varians lika med

$$ V (\ theta \ mid DI) \ approx \ left [-h '' (\ theta_ \ max) \ right] ^ {- 1} $$

($ -h '' (\ theta_ \ max) $ är alltid positivt eftersom vi har en väl avrundat maximalt). Så det betyder att i "vanliga problem" (som är de flesta av dem) är variansen den grundläggande storleken som bestämmer noggrannheten för uppskattningarna för $ \ theta $. Så för uppskattningar baserade på en stor mängd data är standardavvikelsen mycket vettigt teoretiskt - det berättar i princip allt du behöver veta. I princip gäller samma argument (med samma villkor krävs) i flerdimensionellt fall med $ h '' (\ theta) _ {jk} = \ frac {\ partial h (\ theta)} {\ partial \ theta_j \, \ partial \ theta_k} $ är en hessisk matris. De diagonala inmatningarna är också väsentligen avvikelser här också.

Frekvensen som använder metoden med maximal sannolikhet kommer att komma till i princip samma slutsats eftersom MLE tenderar att vara en viktad kombination av data, och för stora sampel Central Limit Theorem gäller och du får i princip samma resultat om vi tar $ p (\ theta \ mid I) = 1 $ men med $ \ theta $ och $ \ theta_ \ max $ utbytt: $$ p (\ theta_ \ max \ mid \ theta) \ approx N \ left (\ theta, \ left [-h '' (\ theta_ \ max) \ right] ^ {- 1} \ right) $$ (se om du kan gissa vilket paradigm jag föredrar: P). Så hur som helst, i parameterberäkning är standardavvikelsen ett viktigt teoretiskt mått på spridning.

"Varför kvadrera skillnaden" istället för "ta absolut värde"? För att svara mycket exakt finns det litteratur som ger skälen till att den antogs och anledningen till varför de flesta av dessa skäl inte håller. "Kan vi inte helt enkelt ta det absoluta värdet ...?". Jag är medveten om litteraturen där svaret är ja, det görs och att det görs är fördelaktigt.

Författaren Gorard säger att för det första användes rutor tidigare för att beräkna enkelhet men att de ursprungliga skälen inte längre gäller. Gorard säger för det andra att OLS antogs eftersom Fisher fann att resultat i analysprover som använde OLS hade mindre avvikelser än de som använde absoluta skillnader (grovt sagt). Således verkar det som om OLS kan ha fördelar under vissa idealiska omständigheter; emellertid fortsätter Gorard att notera att det finns en viss enighet (och han hävdar att Fisher var överens om) att användning av rutor under verkliga förhållanden (ofullständig mätning av observationer, icke-enhetliga fördelningar, studier av en befolkning utan slutsats från ett urval) är sämre än absoluta skillnader.

Gorards svar på din fråga "Kan vi inte helt enkelt ta skillnadens absoluta värde istället och få det förväntade värdet (medelvärdet) av dessa?" är ja. En annan fördel är att användning av skillnader ger mått (mått på fel och variation) som är relaterade till hur vi upplever dessa idéer i livet. Gorard säger att föreställa sig människor som delar upp restaurangräkningen jämnt och vissa kanske intuitivt märker att den metoden är orättvis. Ingen där kommer att kvadrera felen; skillnaderna är poängen.

Slutligen, med absoluta skillnader, noterar han, behandlar varje observation lika, medan däremot kvadrering av skillnaderna ger observationer förutsagda dåligt större vikt än observationer förutsagda väl, vilket är som att låta vissa observationer inkluderas i studien flera gånger. Sammanfattningsvis är hans allmänna inriktning att det idag inte finns många vinnande skäl att använda rutor och att däremot har fördelar med absoluta skillnader.

Referenser:

• Gorard, S. (2005). Översyn av en 90-årig debatt: fördelarna med den genomsnittliga avvikelsen, British Journal of Educational Studies, 53 , 4, s. 417-430.
• Gorard, S. (2013). De möjliga fördelarna med den genomsnittliga absoluta avvikelsen ”effekt” storlek, Social Research Update , 65: 1.

Eftersom kvadrater kan tillåta användning av många andra matematiska operationer eller funktioner lättare än absoluta värden.

Exempel: rutor kan enkelt integreras, differentieras, kan användas i trigonometriska, logaritmiska och andra funktioner, med lätthet .

När du lägger till slumpmässiga variabler läggs deras avvikelser till för alla distributioner. Varians (och därför standardavvikelse) är ett användbart mått för nästan alla distributioner och är inte på något sätt begränsat till gaussiska (även kallade "normala") distributioner. Det gynnar att använda det som vårt felmått. Brist på unikhet är ett allvarligt problem med absoluta skillnader, eftersom det ofta finns ett oändligt antal lika "passar", och ändå är det klart att "en i mitten" är mest realistisk. Även med dagens datorer är beräkningseffektivitet viktigt. Jag arbetar med stora datamängder, och CPU-tid är viktig. Det finns emellertid inget enda absolut "bästa" mått på restprodukter, vilket påpekas av några tidigare svar. Olika omständigheter kräver ibland olika åtgärder.

Naturligtvis kan du beskriva spridningen av en distribution på något sätt meningsfullt (absolut avvikelse, kvantiteter, etc.).

Ett trevligt faktum är att variansen är det andra centrala ögonblicket, och varje fördelning beskrivs unikt av dess ögonblick om de existerar. Ett annat faktum är att variansen är en av två parametrar för normalfördelningen för den vanliga parametriseringen, och normalfördelningen har bara två centrala moment som inte är noll, vilket är dessa två mycket parametrar. Även för icke-normala distributioner kan det vara till hjälp att tänka i ett normalt ramverk.

Som jag ser det är anledningen till att standardavvikelsen finns som sådan att i applikationer uppträder regeln kvadratroten av (som att standardisera en slumpmässig variant), vilket krävde ett namn för den.

Varför kvadrera skillnaden istället för att ta det absoluta värdet i standardavvikelse?

Vi kvadrerar skillnaden mellan x och medelvärdet eftersom det euklidiska avståndet är proportionellt mot kvadratroten av frihetsgraderna (antal x i ett populationsmått) är det bästa måttet på dispersion.

Det vill säga när x-talet har noll betyder $ \ mu = 0 $ :

$$ \ sigma = \ sqrt {\ frac {\ displaystyle \ sum_ {i = 1} ^ {n} (x_i - \ mu) ^ 2} {n}} = \ frac {\ sqrt {\ displaystyle \ sum_ {i = 1 } ^ {n} (x_i) ^ 2}} {\ sqrt {n}} = \ frac {distans} {\ sqrt {n}} $$

Kvadratroten av kvadratsumman är det flerdimensionella avståndet från medelvärdet till punkten i högdimensionellt utrymme som anges av varje datapunkt.

Beräkna avstånd

Vad är avståndet från punkt 0 till punkt 5?

• $ 5-0 = 5 $ ,
• $ | 0-5 | = 5 $ och
• $ \ sqrt {5 ^ 2} = 5 $

Okej, det är trivialt eftersom det är en enda dimension.

Vad sägs om avståndet från punkt (0, 0) till punkt (3, 4)?

Om vi ​​bara kan gå i en dimension åt gången (som i stadsblock) så lägger vi bara till siffrorna. (Detta kallas ibland Manhattan-avståndet).

Men vad sägs om att gå i två dimensioner samtidigt? Sedan (av Pythagoras sats som vi alla lärde oss på gymnasiet), kvadrerar vi avståndet i varje dimension, summerar rutorna och tar sedan kvadratroten för att hitta avståndet från ursprunget till punkten.

$$ \ sqrt {3 ^ 2 + 4 ^ 2} = \ sqrt {25} = 5 $$

Visuellt (se markdown-källan för svaret för koden som ska genereras):

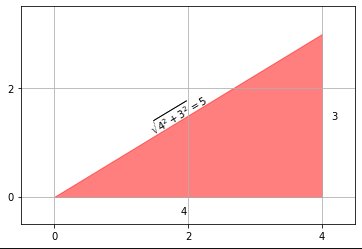
Beräkning av avstånd i högre dimensioner

Låt oss nu överväga det tredimensionella fallet, till exempel vad sägs om avståndet från punkt (0, 0, 0) till punkt (2, 2, 1)?

Det här är bara

$$ \ sqrt {\ sqrt {2 ^ 2 + 2 ^ 2} ^ 2 + 1 ^ 2} = \ sqrt {2 ^ 2 + 2 ^ 2 + 1 ^ 2} = \ sqrt9 = 3 $$

eftersom avståndet för de första två x: erna utgör benet för att beräkna det totala avståndet med det sista x.

$$ \ sqrt {\ sqrt {x_1 ^ 2 + x_2 ^ 2} ^ 2 + x_3 ^ 2} = \ sqrt {x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2} $$

Visas visuellt:

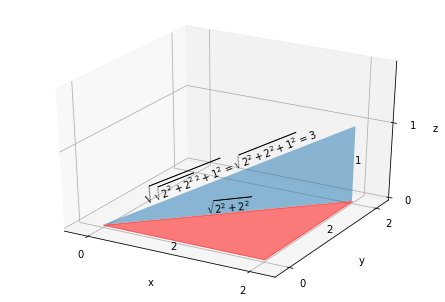
Vi kan fortsätta att utöka regeln om att kvadrera varje dimensions avstånd, detta generaliserar till vad vi kallar ett euklidiskt avstånd, för ortogonala mätningar i hyperdimensionellt utrymme, som så:

$$ avstånd = \ sqrt {\ sum \ nolimits_ {i = 1} ^ n {x_i ^ 2}} $$

och så är summan av ortogonala kvadrater kvadratavståndet:

$$ avstånd ^ 2 = \ sum_ {i = 1} ^ n {x_i ^ 2} $$

Vad gör en mätning ortogonal (eller i rät vinkel) mot en annan? Villkoret är att det inte finns något samband mellan de två mätningarna. Vi skulle leta efter att dessa mätningar är oberoende och individuellt fördelade , ( i.i.d. ).

Varians

Kom ihåg formeln för populationsvarians (från vilken vi får standardavvikelsen):

$$ \ sigma ^ 2 = \ frac {\ displaystyle \ sum_ {i = 1} ^ {n} (x_i - \ mu) ^ 2} {n} $$

Om vi ​​redan har centrerat data vid 0 genom att subtrahera medelvärdet har vi:

$$ \ sigma ^ 2 = \ frac {\ displaystyle \ sum_ {i = 1} ^ {n} (x_i) ^ 2} {n} $$

Så vi ser att variansen bara är kvadratavståndet eller $ distance ^ 2 $ (se ovan), dividerat med antalet av frihetsgrader (antalet dimensioner där variablerna är fria att variera). Detta är också det genomsnittliga bidraget till $ distance ^ 2 $ per mätning. "Genomsnittlig kvadratisk varians" skulle också vara en lämplig term.

Standardavvikelse

Sedan har vi standardavvikelsen, som bara är kvadratroten av variansen:

$$ \ sigma = \ sqrt {\ frac {\ displaystyle \ sum_ {i = 1} ^ {n} (x_i - \ mu) ^ 2} {n}} $$

Vilket motsvarar avståndet , dividerat med kvadratroten av frihetsgraderna:

$$ \ sigma = \ frac {\ sqrt {\ displaystyle \ sum_ {i = 1} ^ {n} (x_i) ^ 2}} {\ sqrt {n}} $$

Genomsnittlig absolut avvikelse

Mean Absolute Deviation (MAD), är ett mått på dispersion som använder Manhattan-avståndet, eller summan av absoluta värden för skillnaderna från medelvärdet.

$$ MAD = \ frac {\ displaystyle \ sum_ {i = 1} ^ {n} | x_i - \ mu |} {n} $$

Återigen, förutsatt att data är centrerade (medelvärdet subtraherat) har vi Manhattan-avståndet dividerat med antalet mätningar:

$$ MAD = \ frac {\ displaystyle \ sum_ {i = 1} ^ {n} | x_i |} {n} $$

Diskussion

• Den genomsnittliga absoluta avvikelsen är ungefär .8 gånger ( faktiskt $ \ sqrt {2 / \ pi} $ ) storleken på standardavvikelse för en normalt distribuerad dataset.
• Oavsett fördelning är den genomsnittliga absoluta avvikelsen mindre än eller lika med standardavvikelsen. MAD underskattar spridningen av en datamängd med extrema värden i förhållande till standardavvikelsen.
• Genomsnittlig absolut avvikelse är mer robust för avvikare (dvs. avvikare har inte lika stor effekt på statistiken som för standardavvikelse.
• Geometriskt sett, om mätningarna inte är ortogonala mot varandra (iid) - om de till exempel var positivt korrelerade, skulle medelavvikelsen vara bättre beskrivande statistik än standardavvikelsen, som förlitar sig på euklidiskt avstånd (även om detta är anses vanligtvis vara bra).

Denna tabell återspeglar ovanstående information på ett mer kortfattat sätt:

$$ \ begin {array} {lll} & MAD & \ sigma \\ \ hline storlek & \ le \ sigma & \ ge MAD \\ storlek, \ sim N & .8 \ gånger \ sigma & 1,25 \ gånger MAD \\ avvikare & robust & påverkad \\ inte \ i.i.d. & robust & ok \ end {array} $$

Kommentarer:

Har du en referens för "genomsnittlig absolut avvikelse är ungefär .8 gånger storleken på standardavvikelsen för ett normalt distribuerat dataset"? Simuleringarna jag kör visar att detta är felaktigt.

Här är tio simuleringar av en miljon prover från standardnormalfördelningen:

  >>> från numpy.random import standard_normal
>>> från numpy import medelvärde, absolut
>>> för _ inom intervallet (10):
... array = standard_normal (1_000_000)
... skriv ut (numpy.std (array), medelvärde (absolut (array - medelvärde (array))))
...
0,9999303226807994 0,7980634269273035
1,001126461808081 0,7985832977798981
0,9994247275533893 0,7980171649802613
0,9994142105335478 0,7972367136320848
1.0001188211817726 0.798021564315937
1.000442654481297 0.7981845236910842
1.0001537518728232 0.7975554993742403
1.0002838369191982 0.798143108250063
0,9999060114455384 0,797895284109523
1.0004871065680165 0.798726062813422
 

Slutsats

Vi föredrar kvadratiska skillnader när vi beräknar ett mått på dispersion eftersom vi kan utnyttja det euklidiska avståndet, vilket ger oss en bättre diskriptiv statistik över dispersionen. När det finns mer relativt extrema värden står det euklidiska avståndet för det i statistiken, medan Manhattan-avståndet ger varje mätning lika vikt.

Ett annat och kanske mer intuitivt tillvägagångssätt är när du tänker på linjär regression kontra median regression.

Antag att vår modell är att $ \ mathbb {E} (y | x) = x \ beta $. Då hittar vi b genom att minimera den förväntade kvadratresten, $ \ beta = \ arg \ min_b \ mathbb {E} (y - x b) ^ 2 $.

Om istället vår modell är att Median $ (y | x) = x \ beta $, så hittar vi våra parameteruppskattningar genom att minimera absoluta resterna, $ \ beta = \ arg \ min_b \ mathbb {E} | y - xb | $.

Med andra ord, om du vill använda absolut eller kvadratfel beror på om du vill modellera det förväntade värdet eller medianvärdet.

Om distributionen till exempel visar sned heteroscedasticitet, är det stor skillnad i hur lutningen för det förväntade värdet $ y $ ändras över $ x $ till hur lutningen är för medianvärdet på $ y $.

Koenker och Hallock har en trevlig bit om kvantil regression, där median regression är ett speciellt fall: http://master272.com/finance/QR/QRJEP.pdf.

Min gissning är detta: De flesta populationer (distributioner) tenderar att samlas kring medelvärdet. Ju längre ett värde är från medelvärdet, desto sällsynta är det. För att på ett adekvat sätt kunna uttrycka hur "out of line" ett värde är, är det nödvändigt att ta hänsyn till både dess avstånd från medelvärdet och dess (normalt sett) medvetenhet om händelse. Kvadrera skillnaden från medelvärdet gör detta, jämfört med värden som har mindre avvikelser. När alla avvikelser har beräknats i genomsnitt är det OK att ta kvadratroten, som återför enheterna till sina ursprungliga dimensioner.

Kvadrering förstärker större avvikelser.

Om ditt urval har värden som finns över hela diagrammet, så för att 68,2% ska ligga inom den första standardavvikelsen måste din standardavvikelse vara lite bredare. Om dina data tenderar att alla faller runt medelvärdet kan σ vara snävare.

Vissa säger att det är för att förenkla beräkningarna. Att använda den positiva kvadratroten på rutan skulle ha löst det så att argumentet inte flyter.

$ | x | = \ sqrt {x ^ {2}} $

Så om algebraisk enkelhet var målet så hade det sett ut så här:

$ \ sigma = \ text {E} \ vänster [\ sqrt {(x- \ mu) ^ {2}} \ höger] $ vilket ger samma resultat som $ \ text {E} \ vänster [| x- \ mu | \ höger] $.

Uppenbarligen kvadrerar detta också effekten att förstärka avlägsna fel (doh!).